Appendix B: The Boltzmann Equation - an outline derivation¶
These notes are derived from those to be found here.
The greatest importance of this equation is its ability to describe non-equilibrium processes.
If there were no collisions at all, a swarm of molecules in phase space would ‘flow’ according to
where \(\mathbf{K}\) denotes an external force and all other symbols have their usual meaning. In this collision-less case, therefore:
where:
and:
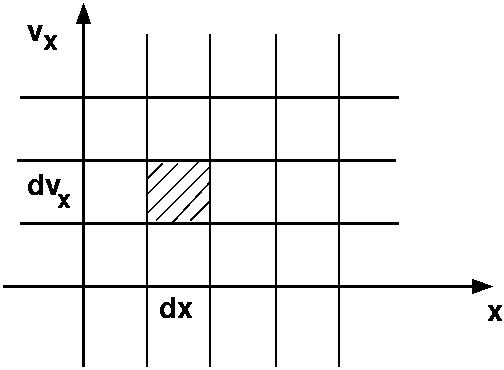
To infer the meaning of equation (2) in the collision-less case, consider flow of gas particles through a thin (effectively one dimensional) pipe. Here, phase-space has only two dimensions, \(x\), and \(v_x\). In the absence of force (i. e. with no change of velocities), let us consider the element of phase-space depicted in Figure 1.
|
Figure 1: A simple phase space for 1D pipe flow |
At time \(t\) the shaded differential volume element contains, on average, \(f (x, v_x) dx dv_x\) particles. The temporal change of \(f (x,v_x)\) is then given by:
To see this, count the particles entering from the left, during interval \(dt\) (assuming \(v_x>0\)):
and those leaving towards the right,
The local change per unit time per unit volume of phase space is then:
Or, more succinctly, we can write:
Hopefully convinced, you will now accept that the above relation is then easily generalized to the case of a non-vanishing force (still in collision-less flow only, note) as follows:
Collisions must affect the equality (1) to (10). A term on the right hand side of equation (1) is the inevitable consequence of this.
The Effect of Collisions¶
A term is now added on the right hand side of (10) to account for the rate at which collisions alter \(f\):
The key is to find an explicit expression for the expression in the right hand side.
Boltzmann solved this critical problem under a rather restrictive set of simplifying assumptions: essentially those assumptions which define the dilute gas limit:
only binary collisions need be considered;
the influence of container walls may be neglected;
the influence of any external force \(\mathbf{K}\) on the rate of collisions is negligible;
velocity and position of a molecule are uncorrelated - the celebrated assumption of molecular chaos. It is believed to be at this point that irreversibility enters our theory.
The effect of the binary collisions is expressed in terms of a differential scattering cross section:
which is the probability density for a certain change of pre and post-collision velocities characterizing the two-particle collision
in which solid angle \(\Omega\) parameterizes the relative orientation of the two vectors
Under the Boltzmann assumptions 1-4 above, the Boltzmann equation takes on the following form:
where
This integro-differential equation describes the spatio-temporal behaviour of a dilute gas. A full derivation of the collision term of (13) may be found in Liboff’s Kinetic Theory.
Given some initial density:
the solution function from (13) tells us how this density changes over time. Since \(f\) has up to six arguments it is difficult to visualize; but there are certain moments of f which represent measurable averages such as the local particle density in 3D space (whose temporal change can thus be computed).
Chapman-Enskog Theory¶
Chapman and Enskog developed a general procedure for the approximate solution of Boltzmann’s equation. For certain simple model systems such as hard spheres their method produces predictions for \(f\) (or its moments) which may be tested in computer simulations.
The initial distribution density may be of arbitrary shape. Let us take all molecules assembled in the left half of a container (think of a removable shutter) and at time \(t = 0\) make the rest of the volume accessible to the gas particles:
where \(f_0\) is the (Maxwell-Boltzmann) distribution density of particle velocities. The subsequent expansion of the gas into the entire accessible volume, and thus the approach to the stationary final state (the equilibrium state) in which the particles are evenly distributed over the volume may be seen in the solution \(f\left(\mathbf{r}, \mathbf{v}; t\right)\). The equilibrium distribution
is that solution of Boltzmann’s equation which is stationary, meaning that:
This is also the limiting distribution for long times, \(t \rightarrow \infty\). It may be shown that this equilibrium distribution is given by:
If there are no external forces such as gravity or electrostatic interactions we have:
In case the temperature is also independent of position, and if the gas as a whole is not moving:
This is the famous Boltzmann distribution; it may be derived also in different ways, without requiring the explicit solution of the transport equation.